本文合作者:laybxc
赛事信息
| 名称 | 出题人 | 开始时间 | 时长 | 官方题解 |
|---|---|---|---|---|
| Codeforces Round #706 (Div. 2) | Daniel_yuan Imakf smg23333 waaitg | Mar/10/2021 20:05 (UTC+8) | 02:00 | Tutorial (en) |
A. Split it!
题目
题目描述
给出一个长度为 的字符串 和一个整数 ,问其能否划分为如下形式:
其中, 表示将 反转得到的字符串。
输入格式
第一行是一个整数 ,表示数据组数。
每组数据第一行有两个整数 ,表示字符串长度和参数 。
每组数据第二行是一个长度为 字符串的 ,由小写字母组成。
输出格式
如果可以合法划分,则输出YES,否则输出NO。
输出大写或小写都可以。
输入输出样例
输入
7
5 1
qwqwq
2 1
ab
3 1
ioi
4 2
icpc
22 0
dokidokiliteratureclub
19 8
imteamshanghaialice
6 3
aaaaaa输出
YES
NO
YES
NO
YES
NO
NO说明/提示
对于第一组数据,一种可能的划分结果为:
对于第二组数据,一种可能的划分结果为:
对于第三组数据,一种可能的划分结果为:
解决方案
思路
注意到 和 互为反转串。
因此,对于一个字符串 ,只要其存在一对长度大于等于 的,互为反转串的前后缀 ,同时中间的非回文串不为空,即满足题意。
代码
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 1050;
int t, n, k;
char s[maxn];
bool check()
{
int i = 1, j = n;
while(s[i] == s[j] && i < j) //找出最长的互为反转串的前后缀
{
i++;
j--;
}
if(i <= j)
{
if(i - 1 >= k) return true; //保证存在合法长度的互为反转串的前后缀的前提下,中间的非回文串不为空
else return false;
}
if(i > j)
{
if(i - 2 >= k) return true; //保证存在合法长度的互为反转串的前后缀的前提下,中间的非回文串不为空
else return false;
}
}
int main()
{
scanf("%d", &t);
while(t)
{
scanf("%d %d", &n, &k);
scanf("%s", s + 1);
if(check())
printf("YES\n");
else
printf("NO\n");
t--;
}
return 0;
}B. Max and Mex
题目
题目描述
定义 为集合 的最大值, 为集合 的最大非负整数值。
给定一个整数集 ,然后将 「把 插入 中」的操作执行 次,求最终 中最后有多少个互不相同的数。
输入格式
第一行一个整数 ,表示数据组数。
每组数据第一行包含两个整数 ,表示集合 的元素个数,以及操作次数。
每组数据第二行包含这 个整数 构成的集合 。
输出格式
输出 次操作之后的集合 中的元素个数。
输入输出样例
输入
5
4 1
0 1 3 4
3 1
0 1 4
3 0
0 1 4
3 2
0 1 2
3 2
1 2 3输出
4
4
3
5
3说明/提示
对于第一组数据,插入 ,最终的集合 为 ,答案为 。
对于第二组数据,插入 ,最终的集合 为 ,答案为 。
解决方案
思路
设 中互不相同的元素个数为 。
先计算第一次操作获得的 ,记为 可分几种情况讨论:
- ,且 在 中存在:
则不论操作多少次, 都不会改变,也不会增加互不相同元素的个数,最终为 。
- ,且 在 中 不 存在:
则不论操作多少次, 都不会改变, 中互不相同的元素个数最终为 。
:
易见,每次操作中, ,最终的 中互不相同的元素个数为
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 100500;
int t, n, k;
int MAX, MEX, MID, cnt;
int a[maxn];
int main()
{
scanf("%d", &t);
a[0] = -1;
while(t)
{
scanf("%d %d", &n, &k);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
}
sort(a+1, a+1+n); //对a[]排序
cnt = 0;
for(int i=1; i<=n; i++)
{
if(a[i] != a[i-1]) cnt++; //计算S中不同元素的个数cnt
}
if(k == 0)
{
t--;
printf("%d\n", cnt);
continue;
}
MAX = a[n]; //获得max
bool flag = true;
for(int i=0; i<=n-1; i++)
{
if(a[i+1] - a[i] >= 2)
{
MEX = a[i] + 1;
flag = false;
break;
}
}
if(flag) MEX = a[n] + 1; //计算mex
if(MEX < MAX)
{
if((MEX + MAX) % 2 == 1) MID = (MEX + MAX + 1) / 2;
else MID = (MEX + MAX) / 2;
flag = false;
for(int i=1; i<=n; i++)
{
if(a[i] == MID)
{
flag = true;
break;
}
}
if(flag) printf("%d\n", cnt); //如果mex<max,且在S中存在,则输出cnt
else printf("%d\n", cnt + 1); //如果mex<max,且在S中不存在,在输出cnt+1
}
else
{
printf("%d\n", cnt + k); //如果mex>max,则输出cnt+k
}
t--;
}
return 0;
}C. Diamond Miner
题目
题目描述
轴上有 个点, 轴上有 个点,将 轴与 轴上的点一一对应地连起来,最小化所有连线的距离。
输入格式
第一行一个整数 ,表示数据组数。
每组数据第一行包含一个整数 ,表示 和 轴上的点数。
接下来 行每行两个整数 表示 和 轴上 个点的坐标。
输出格式
对于每组数据,输出一个实数表示答案。
一般地,设你的答案为 ,标准答案为 ,满足以下条件的答案都可被判定正确:
输入输出样例
输入
3
2
0 1
1 0
0 -1
-2 0
4
1 0
3 0
-5 0
6 0
0 3
0 1
0 2
0 4
5
3 0
0 4
0 -3
4 0
2 0
1 0
-3 0
0 -10
0 -2
0 -10输出
3.650281539872885
18.061819283610362
32.052255376143336说明/提示
对于第一组数据,方案如下,结果为 。
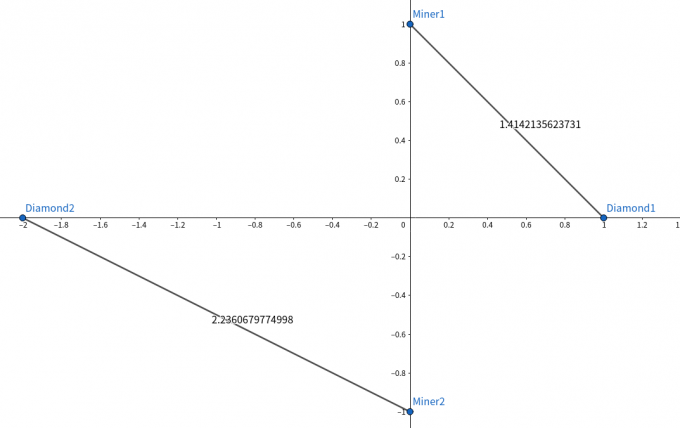
解决方案
思路
贪心做法,每次连接 轴上离原点最近的点和离 轴最近的点即可,时间复杂度 。
证明
MAGIC
代码
#include <iostream>
#include <cstdio>
#include <queue>
#include <cmath>
using namespace std;
const int maxn = 100500;
class Point //定义点类
{
public:
long long x, y, dis;
Point(long long x_, long long y_)
{
x = x_;
y = y_;
dis = sqrt(x * x + y * y);
}
bool operator<(const Point &b) const //重载运算符,使得离原点越近的点在优先队列中越靠前
{
return dis > b.dis;
}
};
int t, n;
double ans;
priority_queue<Point> X, Y; //开两个优先队列,一个用于存在X轴上的点,另一个用于存在Y轴上的点
double P_dis(Point a, Point b) //距离函数,返回两个点之间的欧式距离
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int main()
{
scanf("%d", &t);
while (t--)
{
ans = 0;
while (!X.empty())
X.pop();
while (!Y.empty())
Y.pop();
scanf("%d", &n);
for (int i = 1; i <= n * 2; i++)
{
long long x, y;
scanf("%lld %lld", &x, &y);
Point tmp(x, y);
if (y == 0) //纵坐标为0,说明在X轴上
{
X.push(tmp);
}
if (x == 0) //横坐标为0,说明在Y轴上
{
Y.push(tmp);
}
}
while (X.size() > n) //弹出重复的(0, 0)点
{
X.pop();
}
while (Y.size() > n)
{
Y.pop();
}
while (!X.empty()) //每次选择队首的两个点取欧式距离,加入答案中
{
ans += P_dis(X.top(), Y.top());
X.pop();
Y.pop();
}
printf("%.15lf\n", ans); //根据样例,保留15位小数
}
return 0;
}
D. Let’s Go Hiking
题目
题目描述
有 个格子个格子排成一排,每个格子有一个高度,高度各不相同,即这是一个 的排列。
首先选择一个起点,然后 再选择一个起点。然后 和 两人轮流移动,每次可以往左或往右移动一格。两个人不能同时站在同一格。
只能往比当前位置低的格子移动, 只能往比当前位置高的格子移动。
的位置记为 ,表示在排列中的位置, 的位置记为 ,意义依此类推。
轮到某人时如果他不能移动,则对方获胜。
若两人都采取最优策略,问 要获胜的话有多少种起点选择方案。
输入格式
第一行一个整数,表示参数 。
第二行 个整数 ,表示 的一个排列。
输出格式
输出能使 获胜的起点选择方案数。
输入输出样例
输入 #1
5
1 2 5 4 3输出 #1
1输入 #2
7
1 2 4 6 5 3 7输出 #2
0说明/提示
对于第一组数据, 只能选择从位置 处开始移动,故输出1。
对于第二组数据,如果 选择位置 , 可选择 ,第一轮中 移动到 ,第二轮 移动到 ,第三轮中 只能移动到 ,但是被 堵住了, 卒,故输出0。
解决方案
思路
必须选择一个山顶作为起点,否则如果 选择了和 起点相邻的比 低的点作为起点, 就会被堵住而无路可退。
需要选择下山路径最长的山顶作为起点,因为如果不是最长, 就可以找到一条和 无关的比 下山路径长的上山路径。
当 选择了一个起点, 必须选择 最长下山路径上的一个点为起点,保证 被胁迫着往另一个方向下山,而且和 的距离不能为偶数,否则会被堵住。如果找不到这样的点,则 有必胜策略,否则 有必胜策略。
至此,程序的编写就不难了:
- 先为 找到下山路径最长的山顶作为起点。
- 然后为 找一个最优的起点。
- 此时判断 是否有必胜策略,如果有则输出
0,表明 必输,否则输出1。
没错,你会发现只有0或1两种答案,如果这是OI赛制的题,随机输出就能得 分。
代码
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 100500;
int n, ls, qingshan_spawn, direction, daniel_spawn;
int a[maxn], left_path_length[maxn], right_path_length[maxn];
int dfs(int loc, int pace)
{
int *p = pace == -1 ? &left_path_length[loc] : &right_path_length[loc];
if (loc + pace == 0 || loc + pace == n + 1)
return *p = 0;
if (a[loc] < a[loc + pace])
return *p = 0;
return *p = dfs(loc + pace, pace) + 1;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
}
for (int i = 1; i <= n; i++) //递归找出对于每个点,向左向右的下山路径
{
if (i == 1 && a[i] > a[i + 1])
dfs(i, 1);
else if (i == n && a[i - 1] < a[i])
dfs(i, -1);
else if (a[i] > a[i - 1] && a[i] > a[i + 1])
{
dfs(i, -1);
dfs(i, 1);
}
}
bool flag = true;
for (int i = 1; i <= n; i++) //找出最长的下山路径,并标记为qingshan的起点
{
if (left_path_length[i] == 0 || right_path_length[i] == 0)
continue;
if (left_path_length[i] > ls)
{
ls = left_path_length[i];
qingshan_spawn = i;
direction = -1;
}
if (right_path_length[i] > ls)
{
ls = right_path_length[i];
qingshan_spawn = i;
direction = 1;
}
flag = false;
}
if (flag) //如果没有山顶,即序列单调,则qingshan没有必胜策略
{
printf("0");
return 0;
}
for (int i = 1; i <= n; i++) //如果下山路径最长的路径有起点不同的两条,则qingshan没有必胜策略
{
if (i == qingshan_spawn)
continue;
if (left_path_length[i] == left_path_length[qingshan_spawn] || right_path_length[i] == left_path_length[qingshan_spawn])
{
printf("0");
return 0;
}
if (left_path_length[i] == right_path_length[qingshan_spawn] || right_path_length[i] == right_path_length[qingshan_spawn])
{
printf("0");
return 0;
}
}
if (direction == -1) //找出daniel的起点
{
daniel_spawn = left_path_length[qingshan_spawn] % 2 == 0 ? qingshan_spawn - left_path_length[qingshan_spawn] + 1 : qingshan_spawn - left_path_length[qingshan_spawn];
direction = 1;
}
else
{
daniel_spawn = right_path_length[qingshan_spawn] % 2 == 0 ? qingshan_spawn + right_path_length[qingshan_spawn] - 1 : qingshan_spawn + right_path_length[qingshan_spawn];
direction = -1;
}
if (direction == -1) //比较qingshan和daniel的路径长度,算出结果
{
printf("%d", left_path_length[qingshan_spawn] > daniel_spawn - qingshan_spawn);
}
else
{
printf("%d", right_path_length[qingshan_spawn] > qingshan_spawn - daniel_spawn);
}
return 0;
}

