NVIDIA RTX wallpaper
517 字
3 分钟
【OI考古】数据结构 | 树状数组
树状数组或二元索引树(英语:Binary Indexed Tree,Fenwick Tree),是一种用于高效处理对一个存储数字的列表进行更新及求前缀和的数据结构。
树状数组的元素所管理的序列结构如下图所示:
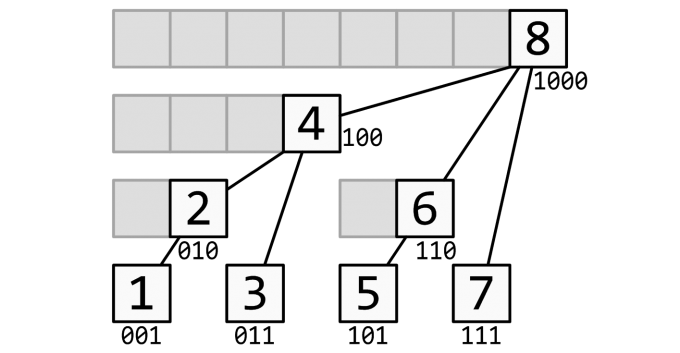
树状数组(单点修改)
模板题:洛谷 P3374 | [模板] 树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
将某一个数加上
求出某区间每一个数的和
输入格式
第一行包含两个正整数 ,分别表示该数列数字的个数和操作的总个数。
第二行包含 个用空格分隔的整数,其中第 个数字表示数列第 项的初始值。
接下来 行每行包含 个整数,表示一个操作,具体如下:
1 x k含义:将第 个数加上2 x y含义:输出区间 内每个数的和
输出格式
输入输出样例
输入
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4输出
14
16说明/提示
【数据范围】
对于 的数据, , ;
对于 的数据, ;
对于 的数据, 。
解决方案
代码
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 500500;
int n, m;
long long c[maxn];
int lowbit(int x)
{
return x & -x;
}
void add(int x, long long k)
{
while (x <= n)
{
c[x] += k;
x += lowbit(x);
}
}
long long query(int x, int y)
{
long long ans1 = 0, ans2 = 0;
x--;
while (x >= 1)
{
ans1 += c[x];
x -= lowbit(x);
}
while (y >= 1)
{
ans2 += c[y];
y -= lowbit(y);
}
return ans2 - ans1;
}
int main()
{
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
{
long long x;
scanf("%lld", &x);
add(i, x);
}
for (int i = 1; i <= m; i++)
{
int op, x, k;
scanf("%d %d %d", &op, &x, &k);
if (op == 1)
{
add(x, (long long)k);
}
if (op == 2)
{
printf("%lld\n", query(x, k));
}
}
return 0;
}

