【OI考古】数据结构 | 线段树

线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。

线段树可以在 $n\log_{}{n}$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树维护的信息，需要满足可加性，即能以可以接受的速度合并信息和修改信息，包括在使用懒惰标记时，标记也要满足可加性（例如取模就不满足可加性，对 $3$ 取模然后对 $4$ 取模，两个操作就不能合并在一起做）。

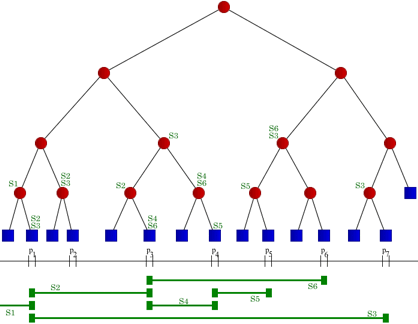
加法线段树#

模板题：洛谷 P3372 | [模板] 线段树 1 #

题目描述#

如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 $k$ 。
求出某区间每一个数的和。

输入格式#

第一行包含两个整数 $n, m$ 分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1 x y k：将区间 $[x, y]$ 内每个数加上 $k$ 。
2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式#

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例#

输入 #1#

输出 #1#

11
8
20

说明/提示#

对于 $30\%$ 的数据： $n \le 8，m \le 10$ 。对于 $70\%$ 的数据： $n \le {10}^3，m \le {10}^4$ 。对于 $100\%$ 的数据： $1 \le n, m \le {10}^5$ 。

保证任意时刻数列中任意元素的和在 $[-2^{63}, 2^{63})$ 内。

解决方案#

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 100500;
int n, m;
long long a[maxn], tree[maxn << 2], lazy[maxn << 2];	//开四倍空间

void pushup(int rt)
{
    tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}

void pushdown(int rt, int ln, int rn)
{
    if (lazy[rt])	//下传lazy标签
    {
        lazy[rt << 1] += lazy[rt];
        lazy[rt << 1 | 1] += lazy[rt];
        tree[rt << 1] += ln * lazy[rt];
        tree[rt << 1 | 1] += rn * lazy[rt];
        lazy[rt] = 0;
    }
}

void build(int l, int r, int rt)
{
    if (l == r)
    {
        tree[rt] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, rt << 1);
    build(mid + 1, r, rt << 1 | 1);
    pushup(rt);
}

void add(int L, int R, int l, int r, int rt, int k)
{
    if (L <= l && R >= r)
    {
        tree[rt] += (r - l + 1) * k;
        lazy[rt] += k;
        return;
    }
    int mid = (l + r) >> 1;
    pushdown(rt, mid - l + 1, r - mid);
    if (L <= mid)
        add(L, R, l, mid, rt << 1, k);
    if (R > mid)
        add(L, R, mid + 1, r, rt << 1 | 1, k);
    pushup(rt);	//每次更新都记得pushup一下
}

long long query(int L, int R, int l, int r, int rt)
{
    if (L <= l && R >= r)
    {
        return tree[rt];
    }
    int mid = (l + r) >> 1;
    pushdown(rt, mid - l + 1, r - mid);
    long long ans = 0;
    if (L <= mid)
        ans += query(L, R, l, mid, rt << 1);
    if (R > mid)
        ans += query(L, R, mid + 1, r, rt << 1 | 1);
    return ans;
}

int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    build(1, n, 1);
    for (int i = 1; i <= m; i++)
    {
        int op, x, y, k;
        scanf("%d", &op);
        if (op == 1)
        {
            scanf("%d %d %d", &x, &y, &k);
            add(x, y, 1, n, 1, k);
        }
        if (op == 2)
        {
            scanf("%d %d", &x, &y);
            printf("%lld\n", query(x, y, 1, n, 1));
        }
    }
    return 0;
}

乘法线段树#

请参阅#

https://oi-wiki.org/ds/seg/