NVIDIA RTX wallpaper
1983 字
10 分钟
【OI考古】图论 | 最近公共祖先 LCA
最近公共祖先简称 LCA(Lowest Common Ancestor)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。
以人的肉眼看来,一棵树上任意两点的 LCA 位置是显然的,然而对于计算机来说,最朴素的算法便是遍历整棵树来寻找 LCA,当询问次数很多的时候,朴素算法的效率将非常低下。本文将介绍几种常见的快速求解 LCA 的算法。
模板题:洛谷 P3379 | [模板] 最近公共祖先(LCA)
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式
第一行包含三个正整数 ,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 行每行包含两个正整数 ,表示 结点和 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 行每行包含两个正整数 ,表示询问 结点和 结点的最近公共祖先。
输出格式
输出包含 行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例
输入 #1
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5输出 #1
4
4
1
4
4说明/提示
对于 的数据, , 。
对于 的数据, , 。
对于 的数据, , 。
样例中的树结构如下:
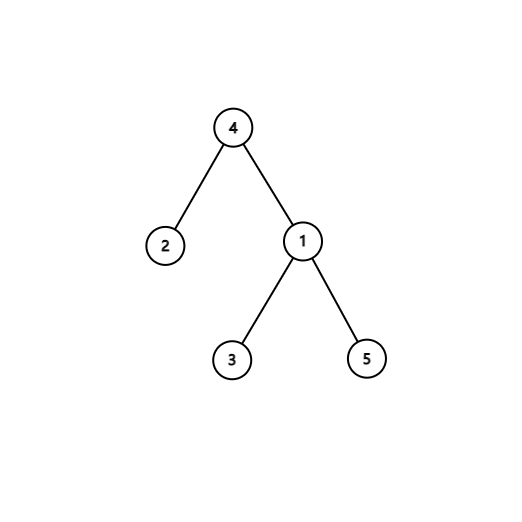
树上倍增
思路:
计算每个节点的深度,保存在
depth[i]数组中。此过程时间复杂度 。计算
fa[i][j]数组,其表示第 个节点的第 个父亲的编号,满足以下性质:利用此性质可以在 过程中初始化 的值,然后逐一计算所有的 。此过程时间复杂度 。
查询 的 过程中,应首先用倍增法,让深度较深的节点跳至与另一节点同一高度,然后二者同事倍增,最后跳到 的子节点,此时 或 的父节点就是 。此过程时间复杂度 。
解决方案
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 500500;
const int maxlog = 20;
int n, m, s, cnt;
int head[maxn], fa[maxn][25], depth[maxn];
struct Node
{
int to, next;
} G[maxn * 2];
void addedge(int u, int v) //链式前向星存图
{
++cnt;
G[cnt].to = v;
G[cnt].next = head[u];
head[u] = cnt;
}
void dfs(int u) //DFS计算出深度,初始化fa[u][0]
{
depth[u] = depth[fa[u][0]] + 1;
for (int i = head[u]; i; i = G[i].next)
{
int v = G[i].to;
if (v == fa[u][0])
continue;
fa[v][0] = u;
dfs(v);
}
}
int lca(int x, int y) //查询LCA
{
if (depth[x] < depth[y]) //钦定x为深度较大的节点,若不然,则交换x, y的值
swap(x, y);
for (int i = maxlog; i >= 0; i--)
{
if (depth[fa[x][i]] >= depth[y]) //如果x往上跳时,深度比y高,说明可以跳
x = fa[x][i];
}
if (x == y) //如果同步深度之后正好在同一节点,说明这就是LCA
return x;
for (int i = maxlog; i >= 0; i--)
{
if (fa[x][i] == fa[y][i]) //如果是第2^i个父节点是同一个,说明跳过头了
continue;
x = fa[x][i]; //如果不是同一个,说明可以跳
y = fa[y][i];
}
return fa[x][0]; //最后x的第1个父节点就是LCA
}
int main()
{
scanf("%d %d %d", &n, &m, &s);
for (int i = 1; i < n; i++)
{
int x, y;
scanf("%d %d", &x, &y);
addedge(x, y);
addedge(y, x);
}
dfs(s);
for (int j = 1; j <= maxlog; j++) //应先固定j,找出所有i的第2^j个父节点,否则会出错
{
for (int i = 1; i <= n; i++)
{
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
for (int i = 1; i <= m; i++)
{
int a, b;
scanf("%d %d", &a, &b);
printf("%d\n", lca(a, b));
}
return 0;
}Tarjan 算法
思路:
利用 Tarjan 算法求 LCA 需要结合并查集。
- 初始化并查集,对于每个节点 ,设 。
- 在 Tarjan 算法的执行过程中,如果当前 DFS 到点 ,先继续 DFS 其子节点 ,再将 设为 。
- 对于以 为根的子树,考察其下的一对 LCA 查询 。若 已经被 DFS 完成,则记录其完成状态,当 DFS 至 时,发现 已被访问,此时使用并查集查询 所属并查集的根节点,由于此时以 为根的子树还没有 DFS 完成,即 ,故查询结果为 本身, 即为 的最近公共祖先 LCA。
解决方案
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn = 500500;
int n, m, s, cnt;
int head[maxn], fa[maxn], ans[maxn];
bool vis[maxn];
vector<int> query_list[maxn], query_id[maxn];
struct Node
{
int to, next;
} G[maxn * 2];
void addedge(int u, int v)
{
++cnt;
G[cnt].to = v;
G[cnt].next = head[u];
head[u] = cnt;
}
int getfa(int x) //查询并查集根节点
{
return fa[x] == x ? x : fa[x] = getfa(fa[x]);
}
void tarjan(int u)
{
vis[u] = true;
for (int i = head[u]; i; i = G[i].next)
{
int v = G[i].to;
if (vis[v])
continue;
tarjan(v); //先DFS每个子节点,再将v划分为u的子节点
fa[v] = u;
}
for (int i = 0; i < query_list[u].size(); i++) //检查所有关于u的询问
{
int v = query_list[u][i];
if (!vis[v] || ans[query_id[u][i]]) //如果询问对应的节点未访问,或者该询问已经被处理过,则跳过
continue; //重复处理询问将导致出错
ans[query_id[u][i]] = getfa(v); //该询问的答案为v的根节点
}
}
int main()
{
scanf("%d %d %d", &n, &m, &s);
for (int i = 1; i < n; i++)
{
int x, y;
scanf("%d %d", &x, &y);
addedge(x, y);
addedge(y, x);
}
for (int i = 1; i <= n; i++)
{
int a, b;
scanf("%d %d", &a, &b);
query_list[a].push_back(b); //保存与每个节点有关的询问,和询问的编号
query_list[b].push_back(a);
query_id[a].push_back(i);
query_id[b].push_back(i);
}
for (int i = 1; i <= n; i++) //初始化并查集
fa[i] = i;
tarjan(s);
for (int i = 1; i <= n; i++)
{
printf("%d\n", ans[i]);
}
return 0;
}数链剖分
思路
先对给出的树进行树链剖分,划分出重轻链,可依托以下几个数组进行划分:
size[]: 表示以 为根的子树的重量,每个节点对子树的贡献为 。son[]: 为 的所有子节点中 , 值最大的 , 称为重链,一条树链由若干连续重链构成。top[]: 表示 所在树链的顶部节点编号。
以上数组可以用两次 DFS 求得。
然后开始求 LCA,对于每对 LCA 的询问 :
- 如果 在同一条树链身上,则 LCA 为深度较浅的节点。
- 如果 不在同一条树链身上,则每次让 的深度较小者跳至其 的父节点,直到两点到达同一条重链,再根据上一条求 LCA 即可。
解决方案
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 500500;
int n, m, s, cnt;
int head[maxn], depth[maxn], size[maxn], son[maxn], top[maxn], fa[maxn];
struct Node
{
int to, next;
} G[maxn * 2];
void addedge(int u, int v)
{
++cnt;
G[cnt].to = v;
G[cnt].next = head[u];
head[u] = cnt;
}
void dfs1(int u) //求depth[], size[], son[]
{
size[u] = 1;
depth[u] = depth[fa[u]] + 1;
for (int i = head[u]; i; i = G[i].next)
{
int v = G[i].to;
if (v == fa[u])
continue;
fa[v] = u;
dfs1(v);
size[u] += size[v];
if (size[v] > size[son[u]])
son[u] = v;
}
}
void dfs2(int u) //求top[]
{
if (son[fa[u]] == u)
top[u] = top[fa[u]];
else
top[u] = u;
for (int i = head[u]; i; i = G[i].next)
{
int v = G[i].to;
if (v == fa[u])
continue;
dfs2(v);
}
}
int lca(int x, int y)
{
while (top[x] != top[y])
{
if (depth[top[x]] < depth[top[y]]) //每次让top值深度较小者上跳至fa[top],直到两者在同一条树链上
swap(x, y);
x = fa[top[x]];
}
return depth[x] < depth[y] ? x : y; //同一条树链上的深度较小者为LCA
}
int main()
{
scanf("%d %d %d", &n, &m, &s);
for (int i = 1; i < n; i++)
{
int x, y;
scanf("%d %d", &x, &y);
addedge(x, y);
addedge(y, x);
}
dfs1(s);
dfs2(s);
for (int i = 1; i <= m; i++)
{
int a, b;
scanf("%d %d", &a, &b);
printf("%d\n", lca(a, b));
}
return 0;
}请参阅
【OI考古】图论 | 最近公共祖先 LCA
https://blog.vonbrank.com/posts/oi-graph-theory-lowest-common-ancestor/

