【OI考古】图论 | 拓扑排序

对于一个有向无环图（DAG），我们要找出一种顶点的排序方式，使得对于图中任意 $u, v$ ，如果 $u, v$ 之间有一条 $u$ 指向 $v$ 的有向路，则 $u$ 排在 $v$ 的前面。这种排序方式被称为拓扑排序（Topological sorting）。

下图是一个 DAG：

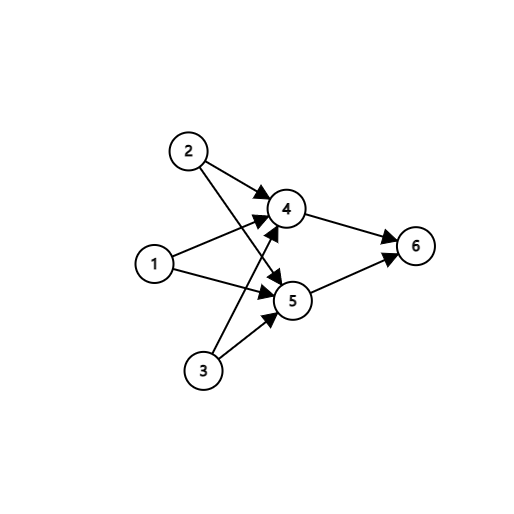
$2, 1, 3, 5, 4, 6$ 是其一个拓扑排序。

模板题#

题目#

P1038 [NOIP2003 提高组] 神经网络

背景#

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述#

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

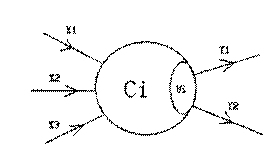
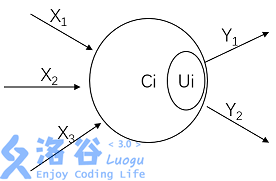
每条边有一个权值，输入点有一个初始权值 $C[i]$ ，非输入点有一个阈值 $U[i]$ ，每个非输入点的 $C[i] = \displaystyle\sum_{j \to i}^{C[j] > 0} C[j] \times w_{i,j}$ ，输出所有输出节点中 $C[i]$ 值大于等于 $0$ 的值。

输入格式#

第一行两个整数 $n, m$ ，表示点数和边数。

接下来 $n$ 行表示每个节点的初始 $C[i], \ U[i]$ 值。

最后 $m$ 行每行三个整数 $u, v, w$ ，表示从 $u$ 指向 $v$ 权值为 $w$ 的边。

输出格式#

输出输出节点的编号及其大于等于 $0$ 的 $C[i]$ 值。

如果没有，则输出 NULL 。

输入输出样例#

输入#

输出#

3 1
4 1
5 1

说明/提示#

解决方案#

思路#

题目实际是一道模拟题，按顺序从输入节点逐层模拟神经网络的前向传播即可。不幸的是，只给出点的邻接关系不足以让我们执行这样的模拟操作，我们需要先对节点进行拓扑排序。

拓扑排序的算法的流程描述非常简洁：

找出图中入度为 $0$ 的点，将其放入已排好的序列末尾。
删除与与该点相关的所有边。
重复上述过程。

显然，这个过程可以开一个队列来实现。

代码#

#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
const int maxn = 110;
int n, m, cc, cnt;
int head[maxn], C[maxn], U[maxn], indegree[maxn], outdegree[maxn], topo[maxn];
queue<int> q;
struct Node
{
    int to, w, next;
} G[maxn * maxn];

void addedge(int u, int v, int w)
{
    ++cc;
    G[cc].to = v;
    G[cc].w = w;
    G[cc].next = head[u];
    head[u] = cc;
}

int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d %d", &C[i], &U[i]);
    }
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        addedge(u, v, w);
        indegree[v]++;
        outdegree[u]++;
    }
    for (int i = 1; i <= n; i++)
    {
        if (!indegree[i])
        {
            q.push(i);
            U[i] = 0;
        }
    }
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        topo[++cnt] = u;
        C[u] -= U[u];
        for (int i = head[u]; i; i = G[i].next)
        {
            int v = G[i].to;
            int w = G[i].w;
            indegree[v]--;
            if (C[u] > 0)
            {
                C[v] += w * C[u];
            }
            if (!indegree[v])
                q.push(v);
        }
    }
    bool flag = true;
    for (int i = 1; i <= n; i++)
    {
        if (!outdegree[i] && C[i] > 0)
        {
            flag = false;
            printf("%d %d\n", i, C[i]);
        }
    }
    if (flag)
    {
        printf("NULL");
    }
    return 0;
}