NVIDIA RTX wallpaper
786 字
4 分钟
【OI考古】数论基础 | 快速幂、最大公约数、线性筛素数
快速幂
以 的情况为例,注意到 ,则 可表示为 ,利用二进制拆分,可以实现在 时间范围内计算出 的值。
模板题:洛谷 P1226 | [模板]快速幂||取余运算
题目描述
给你三个整数 ,求 。
输入格式
输入只有一行三个整数,分别代表
输出格式
输出一行一个字符串 b^p mod k=s,其中 分别为题目给定的值, 为运算结果。
输入输出样例
输入 #1
2 10 9输出 #1
2^10 mod 9=7说明/提示
样例输入输出 1 解释
。
数据规模与约定
对于 的数据,保证 。
解决方案
#include <iostream>
#include <cstdio>
using namespace std;
long long b, p, k;
long long quick_pow(long long base, long long exp, long long mod)
{
if (mod == 1) //任何数模1都等于0
return 0;
if (exp == 0) //任何非零常数的0次方都等于1
return 1;
long long ans = 1;
while (exp)
{
if (exp & 1) //如果末尾为1,则需要乘上该位的指数
{
ans *= base;
ans %= mod; //每步必模
}
base = base * base;
base %= mod;
exp >>= 1;
}
return ans;
}
int main()
{
scanf("%lld %lld %lld", &b, &p, &k);
printf("%lld^%lld mod %lld=%lld", b, p, k, quick_pow(b, p, k));
return 0;
}最大公约数(GCD)
要求 的最大公约数,可使用欧几里得辗转相除法。时间复杂度为
解决方案
#include <iostream>
#include <cstdio>
using namespace std;
long long gcd(long long a, long long b)
{
if (a % b)
return gcd(b, a % b);
else
return b;
}
int main()
{
long long a, b;
scanf("%lld %lld", &a, &b);
printf("%lld", gcd(a, b));
return 0;
}线性筛素数
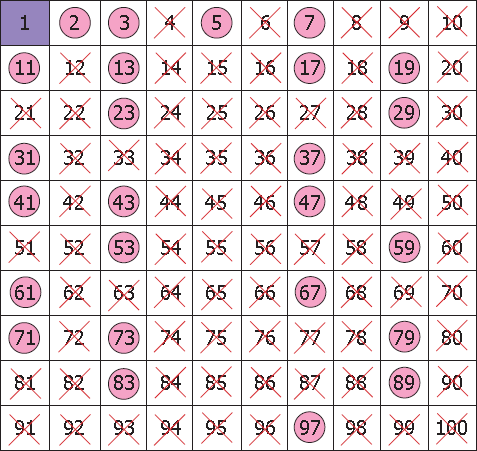
模板题: 洛谷 P3383 | [模板]线性筛素数
题目描述
给定一个范围 ,有 个询问,每次输出第 小的素数。
输入格式
第一行包含两个正整数 ,分别表示查询的范围和查询的个数。 接下来 行每行一个正整数 ,表示查询第 小的素数。
输出格式
输出 行,每行一个正整数表示答案。
输入输出样例
输入 #1
100 5
1
2
3
4
5输出 #1
2
3
5
7
11说明/提示
样例输入输出 1 解释
。
数据规模与约定
对于 的数据, , ,保证查询的素数不大于 。
解决方案
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 100000500;
int n, p, k, cnt;
int prime[maxn / 10];
bool isprime[maxn];
int main()
{
isprime[0] = isprime[1] = true;
scanf("%d %d", &n, &p);
for (int i = 1; i <= n; i++)
{
if (!isprime[i])
{
prime[++cnt] = i;
}
for (int j = 1; i * prime[j] <= n && j <= cnt; j++)
{
isprime[i * prime[j]] = true; //i与小于i的所有素数之积都是合数
if (i % prime[j] == 0) //若i可以整除一个比它小的素数,则停止遍历,保证每个合数只需要标记一次
break;
}
}
for (int i = 1; i <= p; i++)
{
scanf("%d", &k);
printf("%d\n", prime[k]);
}
return 0;
}【OI考古】数论基础 | 快速幂、最大公约数、线性筛素数
https://blog.vonbrank.com/posts/oi-number-theory-quickpow-gcd-eulersieve/

