利用Sympy求解常系数微分方程

昨天接到一个需求，要求用Python实现求解常系数微分方程，虽然后来咕掉了，但是让我发现了Sympy这个科学计算库竟然有如此神奇的功能。本文将介绍如何用Sympy解决初值问题。

先决条件#

Anaconda先决条件#

我们强烈建议您使用免费的Anaconda Python发行版，该发行版为您处理如Numpy, Sympy, Scipy等软件包依赖项提供了一种简便的方法。

你可以参考 {% post_link deploy-anaconda-on-windows 这篇文章 %} 来部署Anaconda。

Sympy先决条件#

SymPy是一个符号计算的Python 库。它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。支持符号计算、高精度计算、模式匹配、绘图、解方程、微积分、组合数学、离散数学、几何学、概率与统计、物理学等方面的功能。

在开始用Sympy求解微分方程之前，不妨先入门一下Sympy。

求微分方程通解#

以初值问题：

$y''+2y'+2y=xe^{-x}, \quad y(0)=y'(0)=0$

为例。

get-general-solution.py可以求出微分方程的通解：

import sympy as sy

f = sy.symbols('f', cls=sy.Function)
x = sy.symbols('x')

# 在这里输入你要求解的微分方程，逗号前输入左式，逗号后输入右式
# 若包含exp(), sin()等函数，请写成sy.exp(), sy.sin()等
differential_equation = sy.Eq(
    f(x).diff(x, 2) + 2 * f(x).diff(x, 1) + 2 * f(x), x * sy.exp(-x))

general_solution = sy.dsolve(differential_equation, f(x)).rhs

print(general_solution)

[out]

(C1*sin(x) + C2*cos(x) + x)*exp(-x)

解初值问题#

get-particular-solution.py可以求出微分方程的特解：

import sympy as sy

x = sy.symbols('x')

C1 = sy.symbols('C1')
C2 = sy.symbols('C2')

# 在这里输入由get-general-solution.py获得的微分方程通解
# 如果出现C3, C4等参数，请在上方加入形如C3 = sy.symbols('C3')等语句
# 若包含exp(), sin()等函数，请写成sy.exp(), sy.sin()等
general_solution = (C1*sy.sin(x) + C2*sy.cos(x) + x)*sy.exp(-x)

# 求解C1, C2等的值，
# 如果初值条件右式不为零，请移项至左边，使得右式为0
# 如果含更多初值条件，请加入形如:
# f3 = general_solution.diff(x, 2).subs(x, 0)
# 等语句，diff(x, n)表示通解对x求n阶导
f1 = general_solution.subs(x, 0)
f2 = general_solution.diff(x, 1).subs(x, 0)
parameters = sy.solve([f1, f2], [C1, C2])

# 如果含有C3，请添加形如：
# particular_solution = particular_solution.subs(C3, parameters[C3])
# 等语句
particular_solution = general_solution
particular_solution = particular_solution.subs(C1, parameters[C1])
particular_solution = particular_solution.subs(C2, parameters[C2])

print(particular_solution)

[out]

(x - sin(x))*exp(-x)

绘制函数图像#

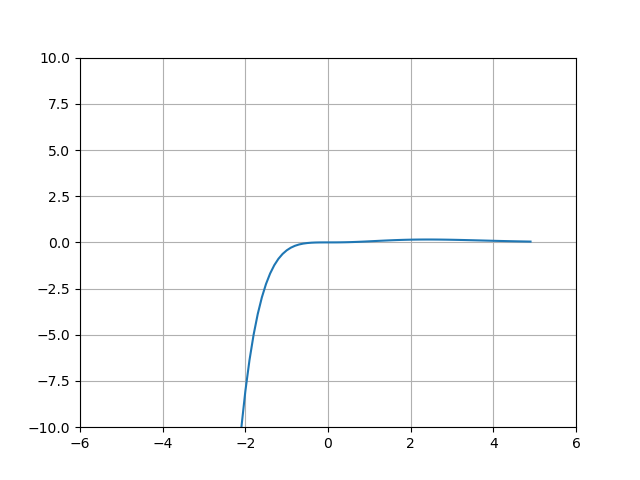
get-function-graph.py可以绘制特解函数的图像：

import sympy as sy
import matplotlib.pyplot as plt
import numpy as np

# 在这里输入由get-particular-solution.py获得的微分方程特解
# 若包含exp(), sin()等函数，请写成sy.exp(), sy.sin()等
x = sy.symbols('x')
particular_solution = (x - sy.sin(x))*sy.exp(-x)

x_range = np.arange(-5, 5, 0.1)	//np.arange(a, b, step)表示绘制的区间和步长
y_range = [particular_solution.subs(x, x_val) for x_val in x_range]
plt.plot(x_range, y_range)
plt.axis([-6, 6, -10, 10])	//axis([x1, x2, y1, y2])表示在[x1, x2], [y1, y2]范围内绘图
plt.grid()
plt.show()

[out]

请参见#

https://blog.csdn.net/cj151525/article/details/95756847
https://www.jb51.net/article/185664.htm
{% post_link deploy-anaconda-on-windows Anaconda部署与使用指南（Windows） %}