本文合作者：laybxc

赛事信息

名称 出题人 开始时间 时长 官方题解
Codeforces Round #706 (Div. 2) Daniel_yuan
Imakf
smg23333
waaitg		 Mar/10/2021
20:05 (UTC+8)		 02:00 Tutorial (en)

A. Split it!

题目

题目描述

给出一个长度为 nn 的字符串 ss 和一个整数 kk ，问其能否划分为如下形式：

s=a1+a2+⋯+ak+ak+1+R(ak)+R(ak−1)+⋯+R(a1)s=a_1+a_2+\dots+a_k+a_{k+1}+R(a_k)+R(a_{k-1})+\dots+R(a_1)

其中， R(x)R(x) 表示将 xx 反转得到的字符串。

输入格式

第一行是一个整数 t(1≤t≤100)t(1≤t≤100) ，表示数据组数。

每组数据第一行有两个整数 n,k(1≤n≤100,0≤k≤⌊n2⌋)n,k(1≤n≤100,0≤k≤⌊\frac n 2⌋) ，表示字符串长度和参数 kk 。

每组数据第二行是一个长度为 nn 字符串的 ss ，由小写字母组成。

输出格式

如果可以合法划分，则输出YES，否则输出NO。

输出大写或小写都可以。

输入输出样例

输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7
5 1
qwqwq
2 1
ab
3 1
ioi
4 2
icpc
22 0
dokidokiliteratureclub
19 8
imteamshanghaialice
6 3
aaaaaa
输出
1
2
3
4
5
6
7
YES
NO
YES
NO
YES
NO
NO

说明/提示

对于第一组数据，一种可能的划分结果为： a1=qw，a2=qa_1 = qw， a_2 = q

对于第二组数据，一种可能的划分结果为： a1=i，a2=oa_1 = i， a_2 = o

对于第三组数据，一种可能的划分结果为： a1=dokidokiliteraturecluba_1 = dokidokiliteratureclub

解决方案

思路

注意到 a1+a2+⋯+aka_1+a_2+\dots+a_k 和 R(ak)+R(ak−1)+⋯+R(a1)R(a_k)+R(a_{k-1})+\dots+R(a_1) 互为反转串。

因此，对于一个字符串 ss ，只要其存在一对长度大于等于 kk 的，互为反转串的前后缀 ，同时中间的非回文串不为空，即满足题意。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 1050;
int t, n, k;
char s[maxn];
bool check()
{
    int i = 1, j = n;
    while(s[i] == s[j] && i < j)	//找出最长的互为反转串的前后缀
    {
        i++;
        j--;
    }
    if(i <= j)
    {
        if(i - 1 >= k) return true;	//保证存在合法长度的互为反转串的前后缀的前提下，中间的非回文串不为空
        else return false;
    }
    if(i > j)
    {
        if(i - 2 >= k) return true;	//保证存在合法长度的互为反转串的前后缀的前提下，中间的非回文串不为空
        else return false;
    }
}

int main()
{
    scanf("%d", &t);
    while(t)
    {
        scanf("%d %d", &n, &k);
        scanf("%s", s + 1);
        if(check())
            printf("YES\n");
        else
            printf("NO\n");
        
        t--;
    }
    return 0;
}

B. Max and Mex

题目

题目描述

定义 max(S)max(S) 为集合 SS 的最大值， mex(S)mex(S) 为集合 SS 的最大非负整数值。

给定一个整数集 SS ，然后将 「把 ⌈max(S)+mex(S)2⌉⌈\frac {max(S) + mex(S)} {2} ⌉ 插入 SS 中」的操作执行 kk 次，求最终 SS 中最后有多少个互不相同的数。

输入格式

第一行一个整数 tt ，表示数据组数。

每组数据第一行包含两个整数 n,kn,k，表示集合 SS 的元素个数，以及操作次数。

每组数据第二行包含这 nn 个整数 a1,a2,…,ana_1, a_2, \dots, a_n 构成的集合 SS 。

输出格式

输出 kk 次操作之后的集合 SS 中的元素个数。

输入输出样例

输入
1
2
3
4
5
6
7
8
9
10
11
5
4 1
0 1 3 4
3 1
0 1 4
3 0
0 1 4
3 2
0 1 2
3 2
1 2 3
输出
1
2
3
4
5
4
4
3
5
3

说明/提示

对于第一组数据，插入 33 ，最终的集合 SS 为 {0,1,3,3,4}\{0,1,3,3,4\} ，答案为 44 。

对于第二组数据，插入 33 ，最终的集合 SS 为 {0,1,3,4}\{0,1,3,4\} ，答案为 44 。

解决方案

思路

设 SS 中互不相同的元素个数为 cntcnt 。

先计算第一次操作获得的 ⌈max(S)+mex(S)2⌉⌈\frac {max(S) + mex(S)} {2} ⌉ ，记为 midmid 可分几种情况讨论：

  1. mid<maxmid < max ，且 midmid 在 SS 中存在：

则不论操作多少次， midmid 都不会改变，也不会增加互不相同元素的个数，最终为 cntcnt 。

  1. mid<maxmid < max ，且 midmid 在 SS 中 不 存在：

则不论操作多少次， midmid 都不会改变， SS 中互不相同的元素个数最终为 cnt+1cnt+1。

  1. mid≥maxmid ≥ max ：

    易见，每次操作中， mid=mex=max+1mid=mex = max + 1 ，最终的 SS 中互不相同的元素个数为 cnt+kcnt+k

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 100500;
int t, n, k;
int MAX, MEX, MID, cnt;
int a[maxn];

int main()
{
    scanf("%d", &t);
    a[0] = -1;
    while(t)
    {
        scanf("%d %d", &n, &k);

        for(int i=1; i<=n; i++)
        {
            scanf("%d", &a[i]);
        }
        sort(a+1, a+1+n);	//对a[]排序
        cnt = 0;
        for(int i=1; i<=n; i++)
        {
            if(a[i] != a[i-1]) cnt++;	//计算S中不同元素的个数cnt
        }

        if(k == 0)
        {
            t--;
            printf("%d\n", cnt);
            continue;
        }

        MAX = a[n];	//获得max
        bool flag = true;
        for(int i=0; i<=n-1; i++)
        {
            if(a[i+1] - a[i] >= 2)
            {
                MEX = a[i] + 1;
                flag = false;
                break;
            }
        }
        if(flag) MEX = a[n] + 1;	//计算mex

        if(MEX < MAX)
        {
            if((MEX + MAX) % 2 == 1) MID = (MEX + MAX + 1) / 2;
            else MID = (MEX + MAX) / 2;
            flag = false;
            for(int i=1; i<=n; i++)
            {
                if(a[i] == MID)
                {
                    flag = true;
                    break;
                }
            }
            if(flag) printf("%d\n", cnt);	//如果mex<max，且在S中存在，则输出cnt
            else printf("%d\n", cnt + 1);	//如果mex<max，且在S中不存在，在输出cnt+1
        }
        else
        {
            printf("%d\n", cnt + k);	//如果mex>max，则输出cnt+k
        }

        t--;
    }
    return 0;
}

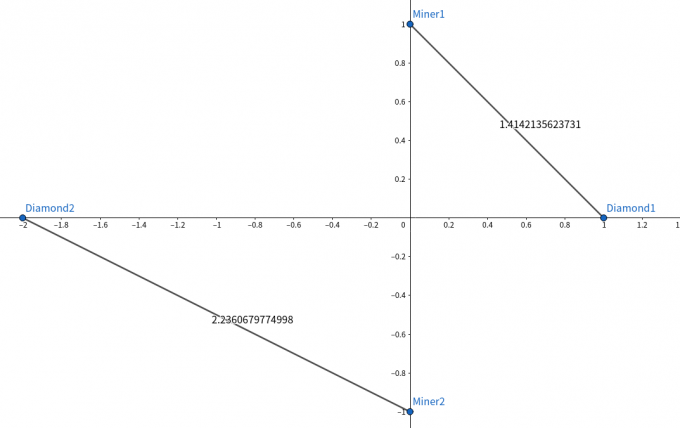
C. Diamond Miner

题目

题目描述

xx 轴上有 nn 个点， yy 轴上有 nn 个点，将 xx 轴与 yy 轴上的点一一对应地连起来，最小化所有连线的距离。

输入格式

第一行一个整数 t(1≤t≤10)t(1≤t≤10) ，表示数据组数。

每组数据第一行包含一个整数 n(1≤n≤105)n(1≤n≤10^5)，表示 xx 和 yy 轴上的点数。

接下来 2n2n 行每行两个整数 x(−108≤x≤108),y(−108≤y≤108)x(-10^8≤x≤10^8), y(-10^8≤y≤10^8) 表示 xx 和 yy 轴上 2n2n 个点的坐标。

输出格式

对于每组数据，输出一个实数表示答案。

一般地，设你的答案为 aa ，标准答案为 bb ，满足以下条件的答案都可被判定正确：

∣a−b∣max(1,∣b∣)≤10−9\frac {|a-b|} {max(1, |b|)} ≤ 10^{-9}

输入输出样例

输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
3
2
0 1
1 0
0 -1
-2 0
4
1 0
3 0
-5 0
6 0
0 3
0 1
0 2
0 4
5
3 0
0 4
0 -3
4 0
2 0
1 0
-3 0
0 -10
0 -2
0 -10
输出
1
2
3
3.650281539872885
18.061819283610362
32.052255376143336

说明/提示

对于第一组数据，方案如下，结果为 2+5\sqrt{2} + \sqrt{5} 。

6xVBB4.md.png

解决方案

思路

贪心做法，每次连接 xx 轴上离原点最近的点和离 yy 轴最近的点即可，时间复杂度 O(nlog⁡n)O(n\log_{}{n}) 。

证明

MAGIC

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <cstdio>
#include <queue>
#include <cmath>
using namespace std;
const int maxn = 100500;
class Point	//定义点类
{
public:
    long long x, y, dis;
    Point(long long x_, long long y_)
    {
        x = x_;
        y = y_;
        dis = sqrt(x * x + y * y);
    }
    bool operator<(const Point &b) const	//重载运算符，使得离原点越近的点在优先队列中越靠前
    {
        return dis > b.dis;
    }
};
int t, n;
double ans;
priority_queue<Point> X, Y;	//开两个优先队列，一个用于存在X轴上的点，另一个用于存在Y轴上的点
double P_dis(Point a, Point b)	//距离函数，返回两个点之间的欧式距离
{
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int main()
{
    scanf("%d", &t);
    while (t--)
    {
        ans = 0;
        while (!X.empty())
            X.pop();
        while (!Y.empty())
            Y.pop();
        scanf("%d", &n);
        for (int i = 1; i <= n * 2; i++)
        {
            long long x, y;
            scanf("%lld %lld", &x, &y);
            Point tmp(x, y);
            if (y == 0)	//纵坐标为0，说明在X轴上
            {
                X.push(tmp);
            }
            if (x == 0)	//横坐标为0，说明在Y轴上
            {
                Y.push(tmp);
            }
        }
        while (X.size() > n)	//弹出重复的(0, 0)点
        {
            X.pop();
        }
        while (Y.size() > n)
        {
            Y.pop();
        }

        while (!X.empty())	//每次选择队首的两个点取欧式距离，加入答案中
        {
            ans += P_dis(X.top(), Y.top());
            X.pop();
            Y.pop();
        }
        printf("%.15lf\n", ans);	//根据样例，保留15位小数
    }
    return 0;
}

D. Let’s Go Hiking

题目

题目描述

有 nn 个格子个格子排成一排，每个格子有一个高度，高度各不相同，即这是一个 1∼n1 \sim n 的排列。

QingshanQingshan 首先选择一个起点，然后 DanielDaniel 再选择一个起点。然后 QingshanQingshan 和 DanielDaniel 两人轮流移动，每次可以往左或往右移动一格。两个人不能同时站在同一格。

QingshanQingshan 只能往比当前位置低的格子移动， DanielDaniel 只能往比当前位置高的格子移动。

QingshanQingshan 的位置记为 xx ，表示在排列中的位置， DanielDaniel 的位置记为 yy ，意义依此类推。

轮到某人时如果他不能移动，则对方获胜。

若两人都采取最优策略，问 QingshanQingshan 要获胜的话有多少种起点选择方案。

输入格式

第一行一个整数，表示参数 n(2≤n≤105)n(2≤n≤10^5) 。

第二行 nn 个整数 p1,p2,…,pnp_1, p_2, \dots, p_n ，表示 1∼n1 \sim n 的一个排列。

输出格式

输出能使 QingshanQingshan 获胜的起点选择方案数。

输入输出样例

输入 #1
1
2
5
1 2 5 4 3
输出 #1
1
1
输入 #2
1
2
7
1 2 4 6 5 3 7
输出 #2
1
0

说明/提示

对于第一组数据， QingshanQingshan 只能选择从位置 x=3x=3 处开始移动，故输出1。

对于第二组数据，如果 QingshanQingshan 选择位置 x=4x=4 ， DanielDaniel 可选择 y=1y=1 ，第一轮中 QingshanQingshan 移动到 x=3x=3 ，第二轮 DanielDaniel 移动到 y=2y=2 ，第三轮中 QingshanQingshan 只能移动到 x=2x=2 ，但是被 DanielDaniel 堵住了， QingshanQingshan 卒，故输出0。

解决方案

思路

QingshanQingshan 必须选择一个山顶作为起点，否则如果 DanielDaniel 选择了和 QingshanQingshan 起点相邻的比 QingshanQingshan 低的点作为起点， QingshanQingshan 就会被堵住而无路可退。

QingshanQingshan 需要选择下山路径最长的山顶作为起点，因为如果不是最长， DanielDaniel 就可以找到一条和 QingshanQingshan 无关的比 QingshanQingshan 下山路径长的上山路径。

当 QingshanQingshan 选择了一个起点， DanielDaniel 必须选择 QingshanQingshan 最长下山路径上的一个点为起点，保证 QingshanQingshan 被胁迫着往另一个方向下山，而且和 QingshanQingshan 的距离不能为偶数，否则会被堵住。如果找不到这样的点，则 QingshanQingshan 有必胜策略，否则 DanielDaniel 有必胜策略。

至此，程序的编写就不难了：

  1. 先为 QingshanQingshan 找到下山路径最长的山顶作为起点。
  2. 然后为 DanielDaniel 找一个最优的起点。
  3. 此时判断 DanielDaniel 是否有必胜策略，如果有则输出0，表明 QingshanQingshan 必输，否则输出1。

没错，你会发现只有0或1两种答案，如果这是OI赛制的题，随机输出就能得 5050 分。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 100500;
int n, ls, qingshan_spawn, direction, daniel_spawn;
int a[maxn], left_path_length[maxn], right_path_length[maxn];
int dfs(int loc, int pace)
{
    int *p = pace == -1 ? &left_path_length[loc] : &right_path_length[loc];
    if (loc + pace == 0 || loc + pace == n + 1)
        return *p = 0;
    if (a[loc] < a[loc + pace])
        return *p = 0;
    return *p = dfs(loc + pace, pace) + 1;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    for (int i = 1; i <= n; i++)	//递归找出对于每个点，向左向右的下山路径
    {
        if (i == 1 && a[i] > a[i + 1])
            dfs(i, 1);
        else if (i == n && a[i - 1] < a[i])
            dfs(i, -1);
        else if (a[i] > a[i - 1] && a[i] > a[i + 1])
        {
            dfs(i, -1);
            dfs(i, 1);
        }
    }

    bool flag = true;
    for (int i = 1; i <= n; i++)	//找出最长的下山路径，并标记为qingshan的起点
    {
        if (left_path_length[i] == 0 || right_path_length[i] == 0)
            continue;
        if (left_path_length[i] > ls)
        {
            ls = left_path_length[i];
            qingshan_spawn = i;
            direction = -1;
        }
        if (right_path_length[i] > ls)
        {
            ls = right_path_length[i];
            qingshan_spawn = i;
            direction = 1;
        }
        flag = false;
    }
    if (flag)	//如果没有山顶，即序列单调，则qingshan没有必胜策略
    {
        printf("0");
        return 0;
    }

    for (int i = 1; i <= n; i++)	//如果下山路径最长的路径有起点不同的两条，则qingshan没有必胜策略
    {
        if (i == qingshan_spawn)
            continue;
        if (left_path_length[i] == left_path_length[qingshan_spawn] || right_path_length[i] == left_path_length[qingshan_spawn])
        {
            printf("0");
            return 0;
        }
        if (left_path_length[i] == right_path_length[qingshan_spawn] || right_path_length[i] == right_path_length[qingshan_spawn])
        {
            printf("0");
            return 0;
        }
    }
    
    if (direction == -1)	//找出daniel的起点
    {
        daniel_spawn = left_path_length[qingshan_spawn] % 2 == 0 ? qingshan_spawn - left_path_length[qingshan_spawn] + 1 : qingshan_spawn - left_path_length[qingshan_spawn];
        direction = 1;
    }
    else
    {
        daniel_spawn = right_path_length[qingshan_spawn] % 2 == 0 ? qingshan_spawn + right_path_length[qingshan_spawn] - 1 : qingshan_spawn + right_path_length[qingshan_spawn];
        direction = -1;
    }


    if (direction == -1)	//比较qingshan和daniel的路径长度，算出结果
    {
        printf("%d", left_path_length[qingshan_spawn] > daniel_spawn - qingshan_spawn);
    }
    else
    {
        printf("%d", right_path_length[qingshan_spawn] > qingshan_spawn - daniel_spawn);
    }

    return 0;
}

请参阅