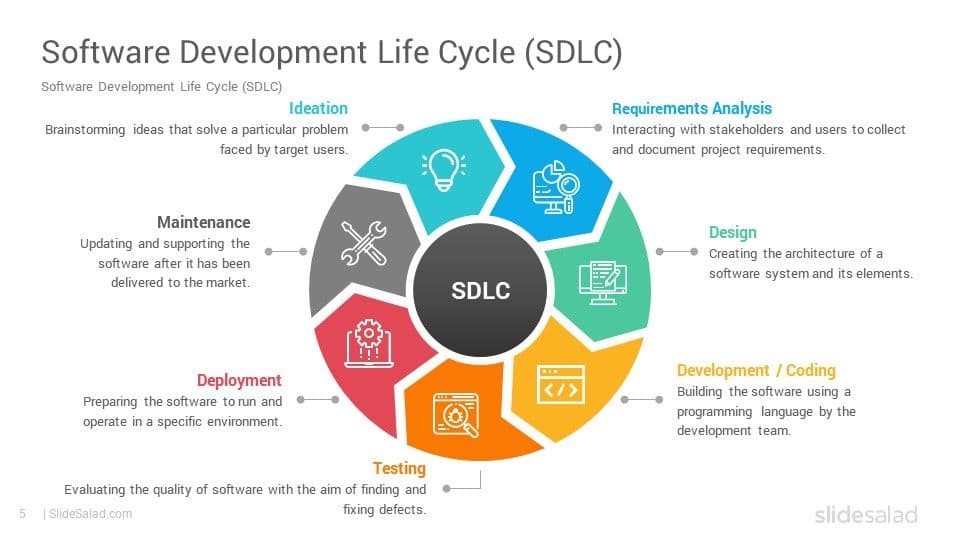
解决单源最短路径问题的几种算法，是Yukko最早给我介绍的几类算法之一。

最短路算法的基本功能，是求解带边权的有向或无向图中任意两点之间最短或最长的路径及其距离。

模板题：洛谷 P4779 | [模板]单源最短路径（标准版）

题目描述

给定一个 nn 个点， mm 条有向边的带非负权图，请你计算从 ss 出发，到每个点的距离。

数据保证你能从 ss 出发到任意点。

输入格式

第一行为三个正整数 n,m,sn, m, s 。 第二行起 mm 行，每行三个非负整数 ui,vi,wiu_i, v_i, w_i ，表示从 uiu_i 到 viv_i 有一条权值为 wiw_i 的有向边。

输出格式

输出一行 nn 个空格分隔的非负整数，表示 ss 到每个点的距离。

输入输出样例

输入 #1
1
2
3
4
5
6
7
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出 #1
1
0 2 4 3

说明/提示

1≤n≤1051≤n≤10^5 ；
1≤m≤2×1051 \leq m \leq 2\times 10^5 ;
s=1s = 1 ；
1≤ui,vi≤n1 \leq u_i, v_i\leq n ；
0≤wi≤1090 \leq w_i \leq 10 ^ 9 ,
0≤∑wi≤1090 \leq \sum w_i \leq 10 ^ 9 。

Floyd 算法

Floyd 算法的时间复杂度为 O(n3)O(n^3) ，比较高，但是常数小，容易实现

ckaPbt.md.png

解决方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1050;
int n, m, s;
int G[maxn][maxn];
int main()
{
    memset(G, 63, sizeof(G));	//初始化为一个大整数
    scanf("%d %d %d", &n, &m, &s);
    for (int i = 1; i <= n; i++)
        G[i][i] = 0;
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        G[u][v] = min(G[u][v], w);	//考虑重边的情况
    }
    for (int k = 1; k <= n; k++)
    {
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                if (G[i][k] + G[k][j] < G[i][j])	//松弛操作
                    G[i][j] = G[i][k] + G[k][j];
            }
        }
    }
    for (int i = 1; i <= n; i++)
    {
        printf("%d ", G[s][i]);
    }
    return 0;
}

Dijkstra 算法

适用于非负权图，但是时间复杂度非常优秀，naive 实现的时间复杂度为 O(n2)O(n^2) ，堆优化能实现 O(nlog⁡n)O(n\log_{}{n}) 的时间复杂度。

ckwk9S.gif

解决方案（naive）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
//dijkstra_naive.cpp
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 100500;
const int INF = 2147483647;
int n, m, s, cnt;
int head[maxn];
long long dis[maxn];
bool vis[maxn];
struct Edge
{
    int to, next, w;
} G[maxn * 5];
void addedge(int u, int v, int w)
{
    ++cnt;
    G[cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void dijkstra_naive(int s)
{
    for (int i = 1; i <= n; i++)
        dis[i] = INF;
    dis[s] = 0;
    for (int i = 1; i <= n; i++)
    {
        int k;
        long long mn = INF;
        for (int j = 1; j <= n; j++)
        {
            if (!vis[j] && dis[j] < mn)
            {
                mn = dis[j];
                k = j;
            }
        }
        vis[k] = true;
        for (int j = head[k]; j; j = G[j].next)
        {
            int v = G[j].to;
            int w = G[j].w;
            if (vis[v])
                continue;
            if (dis[v] > dis[k] + w)
                dis[v] = dis[k] + w;
        }
    }
}
int main()
{
    scanf("%d %d %d", &n, &m, &s);
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        addedge(u, v, w);
    }
    dijkstra_naive(s);
    for (int i = 1; i <= n; i++)
    {
        printf("%lld ", dis[i]);
    }
    return 0;
}

解决方案（堆优化）

解决方案（naive）是不足以通过洛谷的单元最短路径 （毒瘤版） 的，我们需要使用优先队列在 O(log⁡n)O(\log_{}{n}) 时间内找到每次未更新的点集中离已更新点集距离最近的点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
//dijkstra_heap.cpp
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 100500;
const int INF = 2147483647;
int n, m, s, cnt;
int head[maxn];
long long dis[maxn];
bool vis[maxn];
struct Edge
{
    int to, next, w;
} G[maxn * 5];
struct Dis
{
    long long dis;
    int p;

    bool operator<(const Dis &b) const	//重载结构体运算符
    {
        return dis > b.dis;
    }
};

void addedge(int u, int v, int w)
{
    ++cnt;
    G[cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void dijkstra_heap(int s)
{
    for (int i = 1; i <= n; i++)
        dis[i] = INF;
    dis[s] = 0;
    priority_queue<Dis> MinDis;
    Dis tmp;
    tmp.dis = 0;
    tmp.p = s;
    MinDis.push(tmp);
    for (int i = 1; i <= n; i++)
    {
        int k;
        long long mn = INF;

        tmp = MinDis.top();
        while (vis[tmp.p])
        {
            MinDis.pop();
            tmp = MinDis.top();
        }
        mn = tmp.dis;
        k = tmp.p;

        vis[k] = true;
        for (int j = head[k]; j; j = G[j].next)
        {
            int v = G[j].to;
            int w = G[j].w;
            if (vis[v])
                continue;
            if (dis[v] > dis[k] + w)
            {
                dis[v] = dis[k] + w;
                tmp.p = v;
                tmp.dis = dis[v];
                MinDis.push(tmp);
            }
        }
    }
}
int main()
{
    scanf("%d %d %d", &n, &m, &s);
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        addedge(u, v, w);
    }
    dijkstra_heap(s);
    for (int i = 1; i <= n; i++)
    {
        printf("%lld ", dis[i]);
    }
    return 0;
}

SPFA

玄学算法不写（

请参阅